806. Платформы - 3

В старых играх можно столкнуться с такой ситуацией. Герой прыгает по платформам, висящим в воздухе. Он должен перебраться от одного края экрана до другого. При прыжке с платформы на соседнюю, у героя уходит |y₂ – y₁|² энергии, где y₁ и y₂ – высоты, на которых расположены эти платформы. Кроме того, есть суперприём, позволяющий перескочить через платформу, но на это затрачивается 3 * |y₃ – y₁|² энергии.

Известны высоты платформ в порядке от левого края до правого. Найдите минимальное количество энергии, достаточное, чтобы добраться с 1-ой (начальной) платформы до n-ой (последней).

Вход. Первая строка содержит количество платформ n (2 ≤ n ≤ 10⁵). Вторая строка содержит n целых чисел – высоты платформ. Их значения не превышают по модулю 4000.

Выход. Выведите одно целое число – искомую величину энергии.

Пример входа	Пример выхода
4 1 2 3 30	731

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

При заданных функциях энергии герою иногда оптимально будет двигаться назад. Рассмотрим следующий пример. Пусть имеется 4 платформы с высотами 1, 10, 2, 11. Вычислим энергии, которые следует потратить герою для попадания на последнюю платформу при различных вариантах прохода.

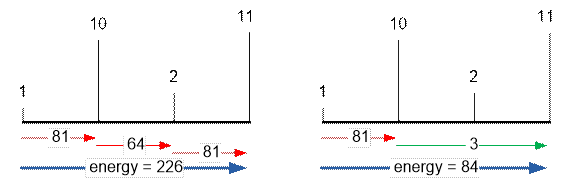
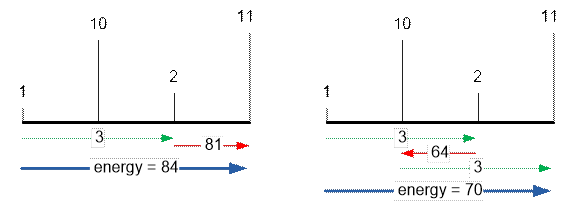
Как видим, оптимально будет прыгнуть с 1 платформы на 3 совершив суперприем, потом вернуться на 2 и при помощи суперприема оказаться на последней, 4 платформе. Общая затраченная энергия равна 3 + 64 + 3 = 70.

Пусть dp[i] хранит наименьшее количество энергии, достаточное, чтобы добраться с 1-й платформы до i-ой. Положим dp[1] = 0, так как сначала мы находимся на первой платформе. На вторую платформу мы можем попасть либо только с первой (если n = 2), либо двумя вариантами:

· с 1 на 2 затратив |y₂ – y₁|² энергии;

· с 1 на 3 и потом на 2 затратив 3 * |y₃ – y₁|² + |y₂ – y₃|² энергии;

Таким образом при n > 2 имеем: dp[2] = min(|y₂ – y₁|², 3 * |y₃ – y₁|² + |y₂ – y₃|²).

Теперь рассмотрим вычисление dp[i]. На i-ую платформу можно попасть либо с (i – 1)-ой либо с (i – 2)-ой использовав суперприем. Однако если i < n, то на i-ую платформу можно попасть с (i + 1)-ой, на которую прыгнули с (i – 1)-ой. То есть dp[i] равно минимум среди:

· dp[i – 1] + |y_i – y_i-1|² : обычный прыжок с (i – 1)-ой платформы;

· dp[i – 2] + 3 * |y_i – y_i-2|² : суперпрыжок с (i – 2)-ой платформы;

· dp[i – 1] + 3 * |y_i+1 – y_i-1|² + |y_i – y_i+1|² : с (i – 1)-ой прыгаем на (i + 1)-ую, а затем на i-ую платформу. Такое передвижение возможно только при i < n.

Реализация алгоритма

Высоты платформ считываем в массив а. В массиве dp храним оптимальные энергии.

#define MAX 100010

long long a[MAX], dp[MAX];

Объявим функцию sq, вычисляющую квадрат числа.

long long sq(long long a)

{

return a * a;

}

Читаем входные данные.

scanf("%d", &n);

for(i = 1; i <= n; i++)

scanf("%lld", &a[i]);

Инициализируем значения dp[1] и dp[2].

dp[1] = 0;

if (n == 2)

dp[2] = sq(a[2] - a[1]);

else

dp[2] = min(sq(a[1] - a[2]), 3 * sq(a[1] - a[3]) + sq(a[2] - a[3]));

Вычисляем значения dp[i] для i ≥ 3.

for(int i = 3; i <= n; i++)

{

dp[i] = min(dp[i - 1] + sq(a[i - 1] - a[i]), dp[i - 2] + 3 * sq(a[i - 2] - a[i]));

if (i < n) dp[i] = min(dp[i], dp[i - 1] + 3 * sq(a[i - 1] - a[i + 1]) + sq(a[i] - a[i + 1]));

}

Выводим ответ.

printf("%lld\n", dp[n]);